Exploring Quantum Computing with Quantum Approximate Optimization Algorithms (QAOA)
We’re constantly trying to integrate the cutting edge technology with our system. Quantum Optimization is a field of solving optimization
problems with the help of quantum computing.
Fundamentals of Quantum Computing
In classical computers, the fundamental unit for computation is bits, where the switch being on represents '1' and the switch being off represents '0'. Any information on those information can be represented in terms of these '1' and '0'. Any operations on it can be achieved through gates.
In case of quantum computers, the fundamental units to represent data are quantum states, which can be constructed using real world physical systems. And operations are done through different linear operators on those states. What makes quantum computers unique is that is some cases it provides speedup in certain algorithms where classical computing at best requires exponential time. The hope of Quantum Approximate Optimization Algorithms is to do so for optimization problems.
Using quantum approximate optimization algorithm (QAOA)
A large class of NP-complete optimization problems including the exact cover (and even many NP-hard problems) can naturally be expressed as the problem of finding the ground state, or minimum energy configuration, of a quantum Ising Hamiltonian.
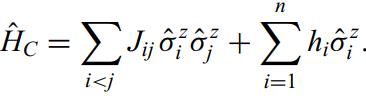
QAOA is a specific case of Variational Quantum Eigensolver (VQE). The VQE allows for the probabilistic measurement of observables over certain classes of parameterized wavefunctions, which can neither be sampled from nor have their properties computed efficiently on conventional devices. it can be shown that in certain scenarios using VQE can speed up the computation of optimization much faster compared to classical counterparts. Any VQE problem can be decomposed into these three parts-
1. A circuit Ansatz
2. A problem specific cost function
3. A training algorithm

1. A circuit Ansatz
An Ansatz would be a circuit of unitary operators which is dependent on parameter which can be tuned acting on a quantum state. This is mostly constructed based on intuition but in many cases the ansatz is fixed by the nature of the problem. In the above image the ansatz would be the circuit Uans . The key aspects of the ansatz are its expressibility and trainability. Which means how well can this ansatz express the system of interest AND how easily can it be trained during update of parameters.
2. Objective cost function
Defines a particular function of interest which we want to minimize or maximize. The cost function is constructed to get a measurement of evaluation of the objective. The idea is to update the parameters of anzatz circuit such that we minimize/maximize the objective cost function. The way it is computed in VQE is we take the expectation value of the operator for that parameter configuration.
3. Training algorithm
The parameters of the ansatz used need to be updated iteratively until convergence. In general, this requires sampling the expectation value of the Hamiltonian several times for a given parameter set in the ansatz in order to define an update rule for the parameters. The new updated parameters are calculated using the Parameters Shift Rule. Based on the observables computed, and the optimization strategy, we can compute and apply updates to the ansatz parameters and begin a new iteration of the VQE.
QAOA applied to tail-assignment problem
The paper of interest focuses on tail-assignment instances where the number of routes is limited as the current quantum capabilities are yet in an infancy stage. Under certain assumptions, like uniquely specifying the start flight of an airline, and some other technical assumptions, the problem (given in Fig-1) can be reduced into a simpler problem called the exact-cover problem. Despite the simplifying assumptions, the exact cover problem is still a relevant case study for many airlines, for example, Air France, has considered the tail-assignment problem to be a pure feasibility problem in the paper[2].
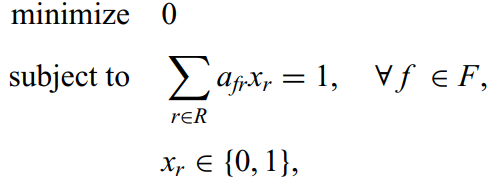
The above Exact-Cover problem can be mapped into a Ising model Hamiltonian. Thus the solution of the problem can be mapped as finding the ground eigenstate of Hamiltonian as given in Fig-2, which in this case is called the Cost-Hamiltonian.
How do we find a solution?
The QAOA starts from taking quantum states like electron spin-states, or atomic states. The initial states are made to evolve through the Hamiltonian of concern. This Hamiltonian are real physical systems which are constructed in labs.
1) Electronic system Hamiltonian: The Hamiltonian is total energy of an arbitrary molecular system defined in terms of its atomic composition.
2) Lattice based Hamiltonian: Hamiltonian is based on atomic configurations, the lattice models assumes a number of sites organized along a lattice.[3]
The Hamiltonian systems form a circuit of quantum gates. The parametrized quantum gates are then optimized in a closed loop using a classical optimizer. The objective of the classical optimizer is to find the optimal parameters that minimize the expectation value of the Cost-Hamiltonian (Fig-2). When the optimal quantum states are found, this state gives us information about the solution of the exact-cover problem.
After simulation, the results indicate that these instances can be solved satisfactorily by means of QAOA, yielding relative high success probabilities. For instance, for the 25-qubit case, the authors have obtained a success probability of 8.97% for p = 2 (in the single measurement scenario). This corresponds to a success probability of 99.9% for 74 repeated measurements. Here the success probability means finding the final quantum states in the ground state which are the right solution for the EC-problem. This means if we make 74 repeated measurements, will find the right solution of the problem as the quantum ground state 99.9% of the time.

QAOA for Examroom
Optimization formulation can be applied to multiple scenarios. In the case of Examroom GIS-evaluator assignment can be mapped into constraint optimization problem. Although GIS-evaluator assignment is much simpler version as there is only basically one variable into consideration. It is still under research stage.
This work is for organization ExamRoom.AI, and thanks for their support to enable us keep doing this research.
References:
[1]: Pontus Vikstål, Mattias Grönkvist, Marika Svensson, Martin Andersson, Göran Johansson, and Giulia Ferrini, Phys. Rev. Applied 14, 034009 (2020).
[2]: Axel Parmentier, Frédéric Meunier, Aircraft routing and crew pairing: Updated algorithms at Air France,
arXiv:1706.06901 (2017).
[3]: Jules Tilly et.al, The Variational Quantum Eigensolver: A review of methods and best practices, Physics Reports, 986, 1-128 (2022).
[4]: Niu, Murphy Yuezhen et al. “Optimizing QAOA: Success Probability and Runtime Dependence on Circuit Depth.” arXiv:1905.12134 (2019).
[5]: https://physlab.org/wp-content/uploads/2023/04/QuantumGD_24100266.pdf
Related Blogs

Exploring Quantum Computing with Quantum Approximate Optimization Algorithms (QAOA)
Exploring Quantum Computing with Quantum Approximate Optimization Algorithms (QAOA) We’re constantly trying to integrate the cutting edge technology with our...
Read More
Decoding RSA-KEM: Bridging to Hybrid Post-Quantum Cryptography
Decoding RSA-KEM: Bridging to Hybrid Post-Quantum Cryptography Linkedin Instagram Over at EXAMROOM.AI, we’re on a non-stop mission to lock down...
Read More
Join the
winning team
A Community of Achievers, Where Dedication, Innovation, and Support Unleash Opportunities for Success and Growth.